How often do you find yourself compelled to give a damn about something worth less than 1%? How about something worth less than .1%? For nearly all Americans math this minute is essentially a rounding error. Could it possibly be that such a rounding error could POSSIBLY impact our retirements in a meaningful fashion? In a recent conversation with a colleague I found out the answer and more...
(A note before we
begin: when I finally finished my undergrad in English a clever family member
gave me a coffee mug that read, “I’m an English major, you do the math.” We’re
going to get into some math today. If you think I’ve made a mistake in my
arithmetic, let me know! Give me a holler in the comments below the article and
I’ll be happy to adjust. And you can bet I’ll be blaming that English degree…)
The Setup
Recently I was reviewing how a tax advantaged retirement
account was doing. A few interested colleagues started asking some questions
about the account and what types of things I prefer to invest in. That, of
course, led to me talking about the impact of fees (you’ll recall I first
covered those when I talked about the types of things to look for when investing). Someone asked
what I was paying in fees to compare to their own account.
Per my preference I’m heavily invested in low-cost stock
indexes. The total fees for maintaining my investments in the particular
account I was looking at were .07%. That’s pretty solid in the modern index
fund driven retirement investment world. My colleague’s? They had left their
investment in the default account available when he had first been hired and
the fee structure was a bit higher at .97%. The question we had for one
another: how much difference could that increase actually make? After all, we’re
talking about a fraction of a fraction, a portion of a percentage. Is .0007
really that much different than .0097?
The Math
The fees we pay on our accounts, and likely the ones you pay
on your employer-sponsored retirement accounts, are based on the assets in them
and are represented as a percentage. For me that was .07%, or .0007, or $.70 in
fees for every $1,000 I have saved. For my colleague? His was .97% or .0097, or
$9.70 in fees for every $1,000 he had invested. The difference? My coworker pays approximately ten times
what I do in fees!
So what’s the big deal? After all, he’s only paying $10
while saving $1,000, far more money. The
trick is to step back and look at the cost of those higher fees at greater levels
of savings. From that vantage point it becomes clear very quickly just how
impactful this rounding error of a difference in fees can be. At $10,000 in
savings I pay $7 in fees. My colleague? $97. Once we reach $100,000 in savings I
pay $70 in fees while my colleague pays $970. He’s paying nearly $1,000 each
year for the same services I am but for no greater advantage. At $1,000,000,
about the amount either of us might need to retire with some amount of comfort,
he’d be paying $9,700 every year to manage his money. Me? Just $700.
Even a rounding error in fees can be the equivalent of
thousands of dollars each year in savings or capital to spend!
Compounding the Damage
Believe it or not, it actually gets worse (much worse). The
most insidious part of these fees is that they harness the most powerful force in the universe and stack it against us. It’s
not enough to simply account for the lost savings from the difference in fees
between my account with lower fees and my colleague’s with the higher fees. You
also have to account for the compounding rate of return that money would have made
for you instead of your investment firm if you’d been able to keep it working
on your behalf instead of theirs.
To calculate the difference we’re going to set some rules
for both accounts to ensure the comparison is equivalent:
- · The investment time period for the accounts is 30 years
- · The amount invested each year is $18,000, the max for your 401k (we’re not going to adjust this number for this case study, though it’s likely that over time the cap on 401k’s will go up)
- · The rate of return for the invested assets is 7%, about what the 100 year rate of return on the S&P 500 has been
- · As a “control,” we’ll look at an account with a 0% fee as well
Where do we end up? Here’s the breakdown in handy dandy
chart form:
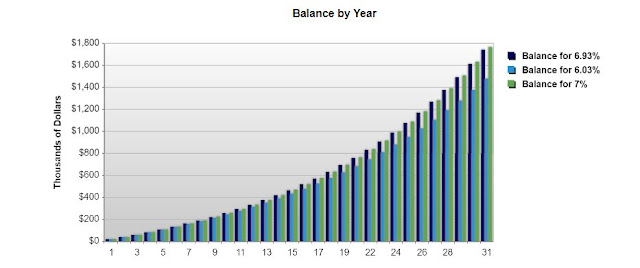 |
| CLICK GRAPH TO ZOOM IN |
And here’s a look at the raw numbers:
.00% Fee
|
.07% Fee
|
.97% Fee
|
|
Total After 30 Years
|
$1,764,097.18
|
$1,741,411.27
|
$1,476,892.84
|
Difference from 0% Fee
|
$0
|
$22,685.91
|
$287,204.34
|
Difference from .07% Fee
|
N/A
|
$0
|
$264,518.43
|
After all the calculations are complete I’m paying about
$23,000 over 30 years to a financial firm for the privilege of handling the
bookkeeping for my 401k account compared to an account with no fees. Of course
I’d love that number to be lower, but at the end I’m very comfortable with $1.7
million in retirement. My colleague? Ho boy.
For just .97% in fees my colleague has $1,476,892.84 at
retirement, well over a quarter million dollars less than either my account or
the hypothetical free account. Over the course of 30 years he paid a money
manager more than the median cost of an American home just for parking his
money for him. Imagine! By taking the lower fee I essentially got a free
retirement home for my efforts while my colleague will have to come up with a
different solution for drinking piña coladas by a golf course in
Phoenix. The math is clear: even a tiny rounding error can powerfully impact
the state of your retirement accounts.
The Solution
I’ve said it time and time again: when you invest, make sure
to look for the funds your employer offers with the lowest fees. Anything 1% or
higher is tantamount to highway robbery; you’re not getting much value for that
fee, so you might as well keep more of that money for yourself and have it
compound in your favor, not the big banks’. Full disclosure where it’s due: I’m
not the person who invented this idea. Far greater minds than mine have been
championing it for years. John Bogle, the inventor (effectively) of the index
fund for casual investors like you and me, has long focused the investment firm
he founded on reducing fees to keep handing better returns to investors. Even
sometimes-world’s-richest-man Warren Buffett, largely credited as being the
greatest investor of all time, has declared to his shareholders, “When
trillions of dollars are managed by Wall Streeters charging high fees, it will
usually be the managers who reap outsized profits, not the clients.” We’re
definitely not smarter than Warren Buffett, so why not follow his advice?
Something I do want to note: fees in employer managed
retirement funds can be somewhat dependent on the size of the employer. The
smaller your company is the likelier it is that you will have higher fees as
your negotiating power as a group is lessened. If 100 people save $10,000,000
together they can “buy in bulk” much less than 1,000 people who’ve saved
$100,000,000. The end result? The company of 100 people is more likely to get .97%
while the 1,000 folks benefit from .07%. Look on the bright side if that’s your
current spot: across the industry fees have been plummeting in recent years as
companies drop them further and further to compete for clients.
The Exception to the Rule
The moral of this story is absolutely to focus on finding
the lowest fees possible in your retirement accounts. However there is one possible exception to this rule:
specific asset class requirements. What I mean is that if you’re close to
retirement being fully exposed to the stock market might put your account at
risk of having big swings which can be harmful if you plan on relying on that
income in the near future. Paying a higher fee of .97% for an account that
automatically manages your assets across bonds and stocks to ensure you have a
stable mix to balance your retirement may be a fine tradeoff. Additionally
earlier in your career an all bonds fund with a .07% fee compared to a stock
index at .97% might mean you’re better with the .97% fee because you need to
make riskier investments with a higher rate of return as you’ve got 30 years
left of saving to do.
For me? I’ll stick with my .07% and re-allocate on my own
every few years as necessary. I’m just not willing to pay someone $1,000 for
every $100,000 I’ve invested to do that for me, even if it is just a "rounding error."
No comments:
Post a Comment